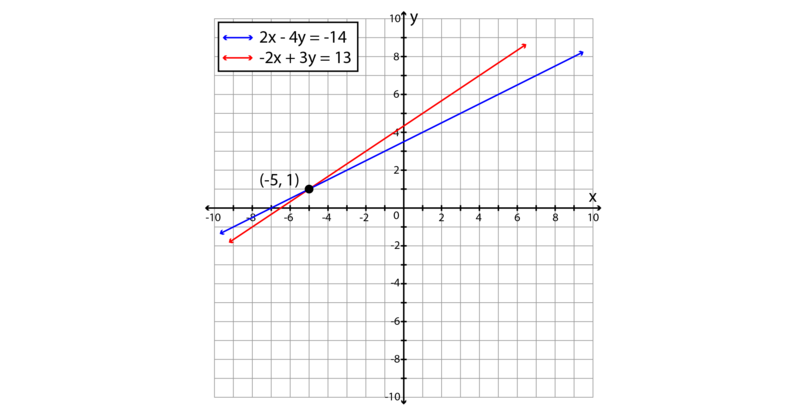
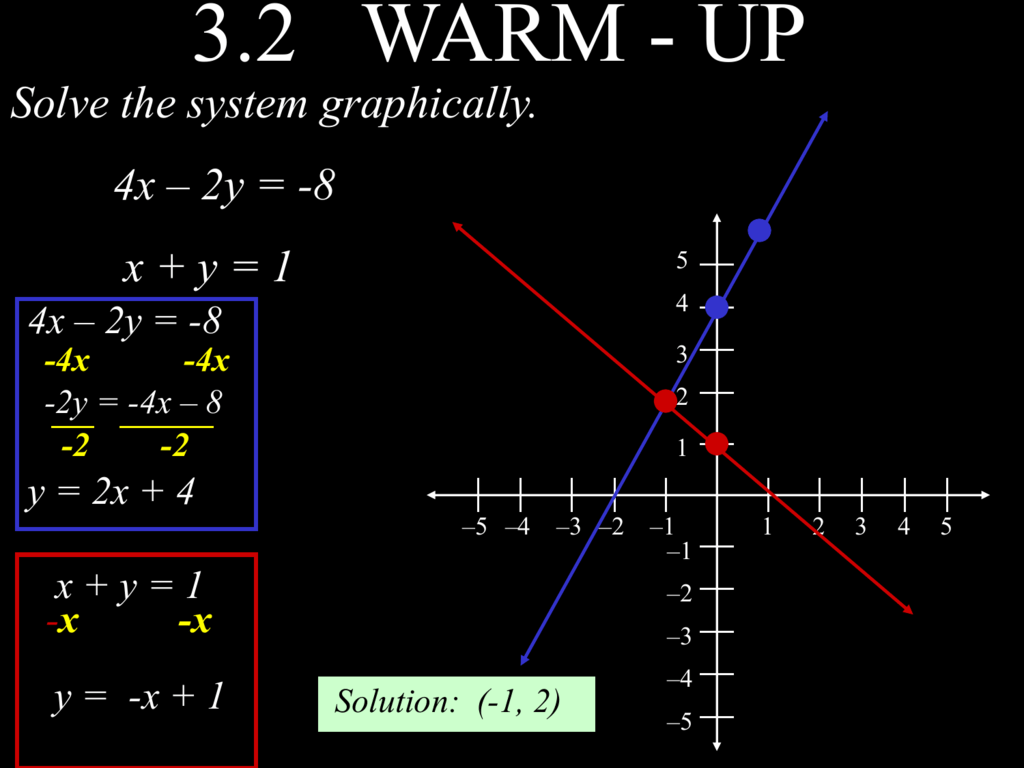
6 2 Elimination Method Simultaneous Linear Equations Siyavula
Ex 34, 1 (Elimination)Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving3x 3y z = 0 Question Learn about linear systems, the GaussJordan elimination method, and
X+2y=3/2 2x+y=3/2 by elimination method
X+2y=3/2 2x+y=3/2 by elimination method-Or click the example About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding orThe elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first

Ex 4 6 11 Solve Using Matrix Method 2x Y Z 1 X 2y Z 3 2 3y 5z 9
Solve the following systems of linear equations by Gaussian elimination method 2x 4y 6z = 22, 3x 8y 5z = 27, − x y 2z = 2 Solution x 2y 3z = 11 (1) 2y 4z = 6 (2) 22z = 44 z = 2 By applying the value of z in (2), we get 2y 4 (2) = 6Solve the Given equation in Elimination method and Substitution Method印刷√ x 2y=3/2 2x y=3/2 by elimination method X2y=3/2 2xy=3/2 by elimination method
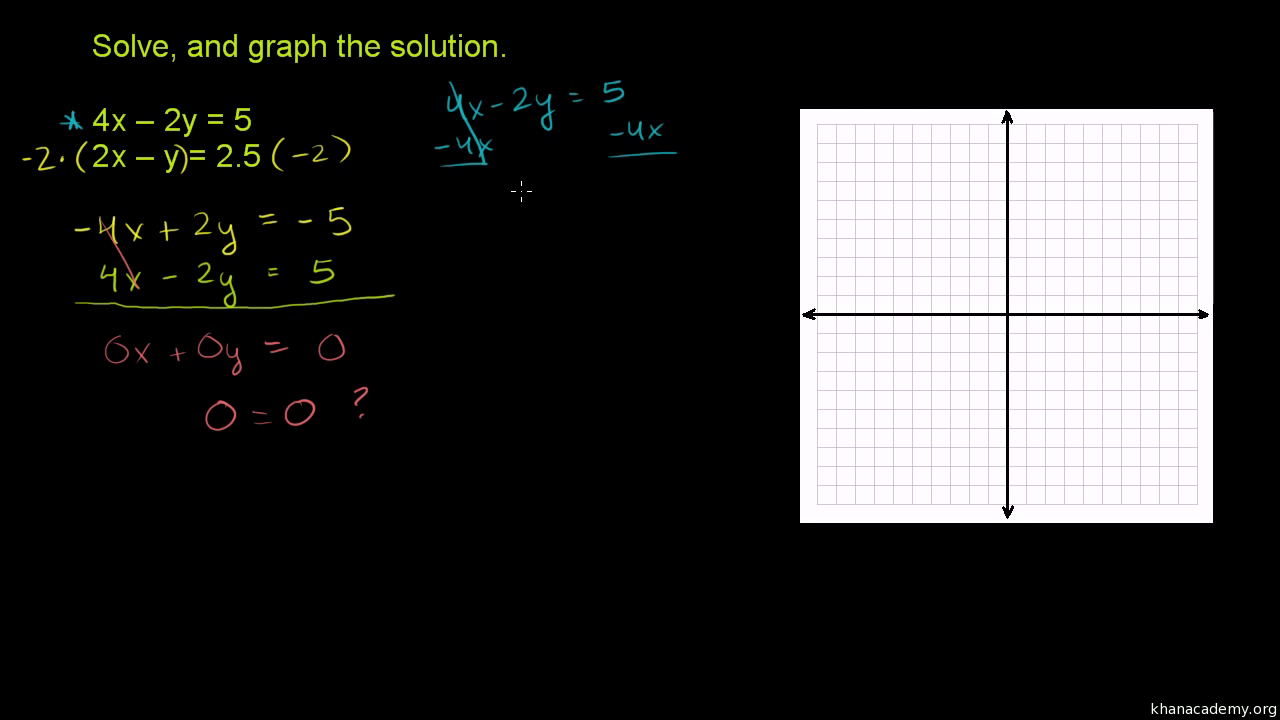
\\begin{aligned}&x2y=10\\&2xy=5\end{aligned}\ > X+2y=3/2 2x+y=3/2 by elimination methodのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します「X+2y=3/2 2x+y=3/2 by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
The trick with Gaussian elimination is to find the leading element (circled) at from the starting matrix and new matrix at each step To find value of x & y by elimination method 2x 4y = 3 (1) 4x 2y = 3 (2) Do this to eliminate x, 2 × eqn (1) eqn (2) 4x 8y ( 4x 2y ) = 6 3 8y 2y = 3 6y = 3 Do this to eliminate y, 2 × eqn (2) eqn (1) 8x 4y ( 2x 4y ) = 6 3 8x
Incoming Term: x+2y=3/2 2x+y=3/2 by elimination method,










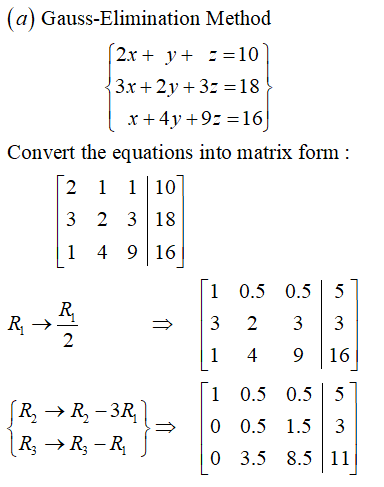





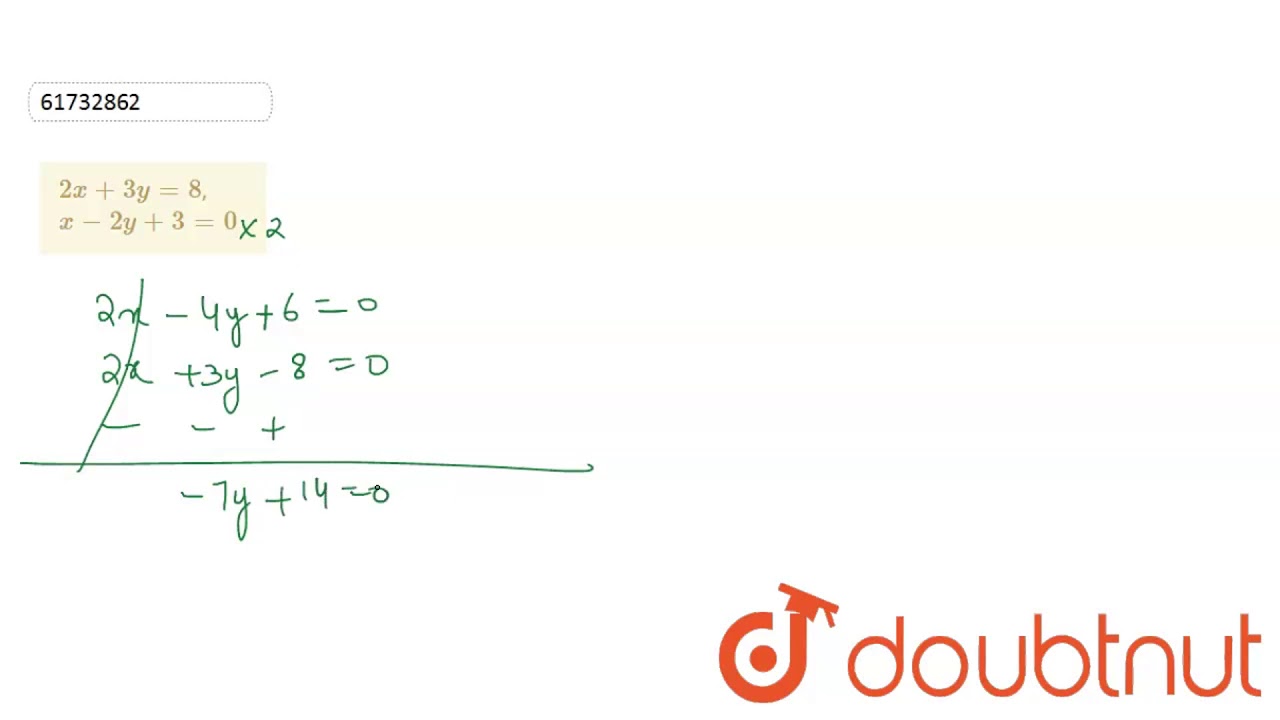


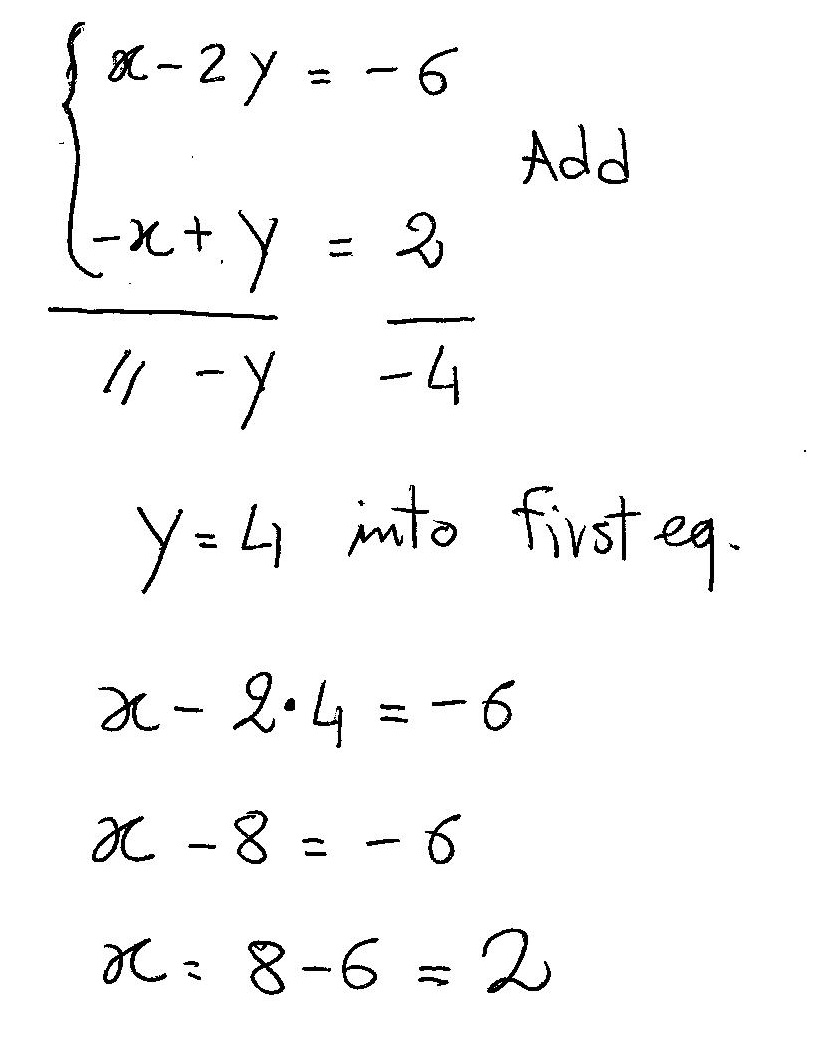




























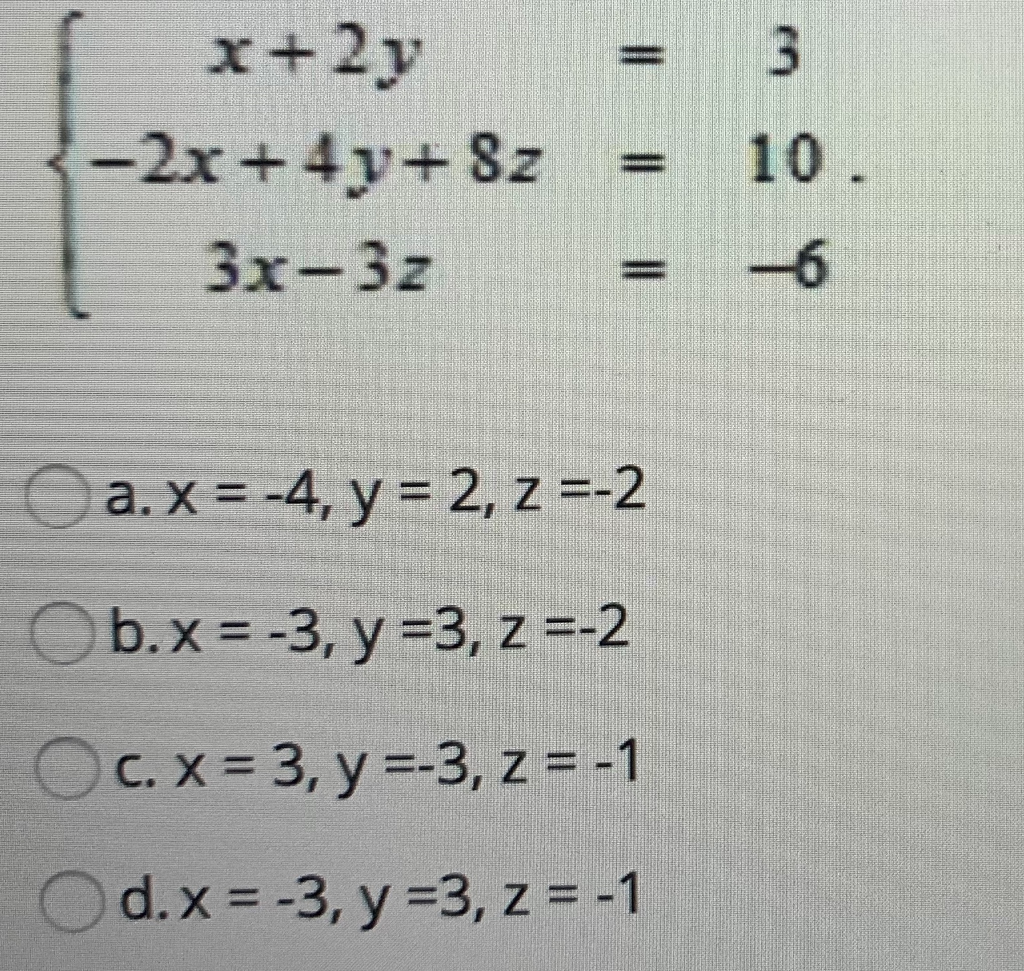










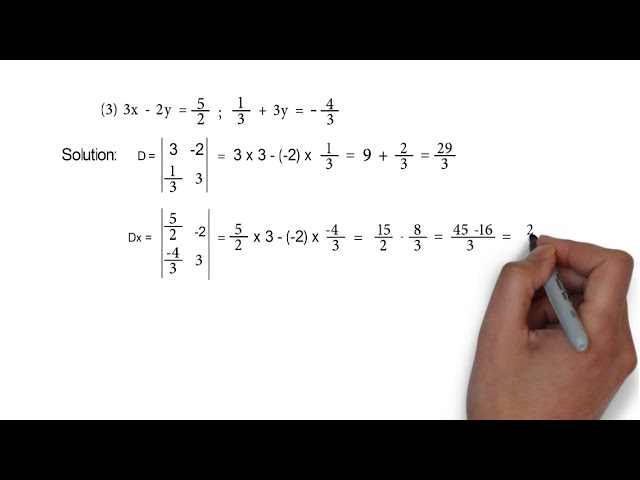
























0 件のコメント:
コメントを投稿